2022智慧上进理数答案第九

2022智慧上进理数答案第九，目前我们已经整理了2022智慧上进理数答案第九的各科答案和试卷，更多智慧上进请关注本网站。

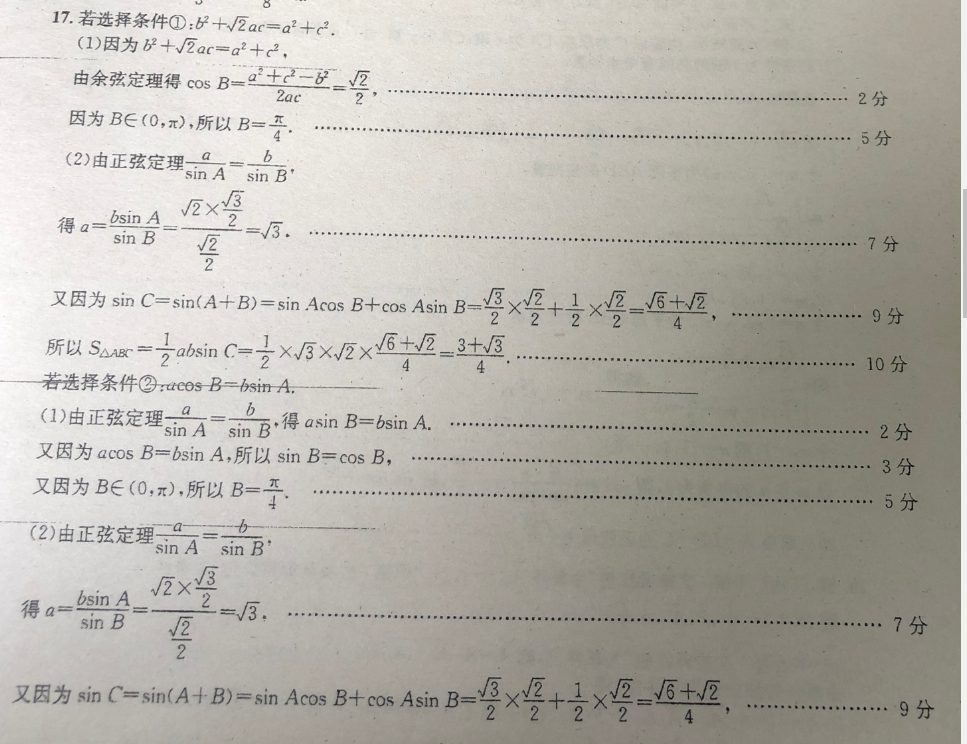
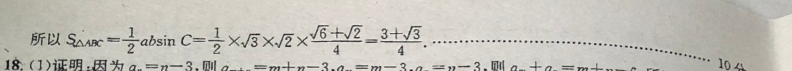
17.若选择条件①:b2+√2ac=a2+c2(1)因为b2+√2ac=a2+c2由余弦定理得cosB=92+c-bZa2分因为B∈(0,x),所以B=5分(2)由正弦定理sin A sin B得a=iA2xsIn√3又因为sinC=in(A+B)= Fsin Acos B+c0 s Asin B=×2+1×2=6+所以S△=iC=2X3x×6+E=3+③10分若选择条件②:eosB= sin A(1)由正弦定理-=bAsinB·得 asin B= bsin A.…又因为 acos B= bsin a,所以sinB=cosB,3分又因为B∈(0,x),所以B=分(2)由正弦定理 in A sin B2√3得BvaV分又团为如C一mA+B)=AsB0AmB=×+1x2=+2分所以S△A=1 absin C=1×××6+23+

20.解:(1)记“甲第i次抢得红包”为事件A,(i=1,2),“甲第次没有抢得红包”为事件A1则P(A1)=女,P(A1)23记“甲恰有1次抢得红包”为事件A,则A=A1A2+A1A2,由事件的独立性和互斥性,得P(A)=P(A1A2+A1A2)=P(A1A2)+P(A1A2)=P(A1)P(A2)-P(A1)P(A2)…4分3×3+3×3=9·(2)记乙第i次抢得红包”为事件B(i=1,2,3),“乙第i次没有抢得红包”为事件B分周PB)=3,P)=2由题意知X的所有可能取值为0,5,10,15,20,由事件的独立性和互斥性,得Px-0)=PBBB)=(22Px5-P(BE瓦+瓦B)=2X吉×(号y=器x=10PB高十国BB)=(x景+(y×一Px=15)=P(BBB+BB)=2X(3)×2一P(X=20)=P(BBB)=(3)=1所以X的分布列为(每正确求出一个P的值,得1分)10152024P10分所以乙抢得所有红包的钱数之和X的数学期望E(X)=0×9+5×5+10×2+15×3+20×1=2012分