20222020智慧上进数学八答案

20222020智慧上进数学八答案，目前我们已经整理了20222020智慧上进数学八答案的各科答案和试卷，更多智慧上进请关注本网站。

1L.ACD【试题情境】本题是综合性题目,属于课程学习情境和探索创新情境,具体是数学运算学习情境和数学探究情境【关键能力】本题考查逻辑思维能力、运算求解能力【解析】对于A选项,由题意知∫(-1)=0,则g(-1)=f(f(-1))=f(0)=0所以A选项正确对于B选项,令∫(xu,则求g(x)=(f(x))=2的根,即求f(u)=2的根,作出函数f(x)的大致图象如图所示,由图可知方程f(u)=2没fx有实根,所以g(x)=2没有实根所以选项B错误对于C选项,令u=f(x),则1=-2,u<0,方程g(x)=-2,即f(u)=-2,得2,n20,得u1=-3u2=1+3,方程f(x)=u1得x+1=-3(x<0)或-x2+2x=-3(x≥0),解得x=-4或x=3.易知方程(x)=l2没有实数根所以方程g(x)=-2的所有根之和为-1,选项C正确对于D选项,当x<0时,g(x)=f(x+1),则将函数f(x)在(-a,1)的图象向左平移1个单位长度可得函数g(x)的图象,由图可得当x<0时,函数g(x)的图象不在∫(x)的图象的下方,所以D选项正确.故选ACD方法技巧》对于分段函数,已知函数的值求自变量的值时;常常先根据每一段的解析式分别求解,但要注意检验所求自变量的值是否符合相应段的自变量的取值范圈,然后将各段的结果求并集即可如果分段函数的图象易得,也可以作出函数图象,然后结合图象求解

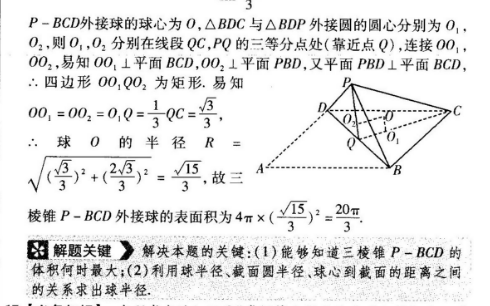
2016.3【关键能力】本题考查逻輯思维能力、空间想象能力【学科素养】试题借助三棱锥与外接球之间的关系,考查球半径、截面圆半径与球心到截面的距离之间的关系,需要考生将空间问题平面化,增强了考生运用几何直观和空间想象思考问题的意识,考查的学科素养是理性思维、数学探索【解题思路】先根据题意分析出当平面PBD⊥平面BCD时三棱锥P-BCD的体积最大,然后取BD的中点Q,连接PQ,QC,根据已知条件求出三棱锥P-BCD体积最大时△BDC与△BDP的外接圆半径,设三棱锥P-BCD外接球的球心为O,△BDC与△BDP外接圆的圃心分别为O,O2,连接OO1,OO3,得到四边形OO1QO2为矩形,最后借助球半径、截面圆半径、球心到截面的距离之间的关系求出外接球半径,即可得解【解析】易知当平面PBD⊥平面BCD时三棱锥P-BCD的体积最大如图,当平面PBD⊥平面BCD时,取BD的中点Q连接PQ,QC,则PQ⊥BD,PQ=QC,平面PBD∩平面BDC=BD,PQ⊥平面BDC,PQ⊥QC,∴PC=PQ2+0C=2PQ2=6,PQ=CQ=3,又△BDC与△BDP为等边三角形,BD=2.设△BDC与△BDP的外接圆半径分别为n1,r2,由正弦定理可得2r1=2r,=-243设三棱锥P-BCD外接球的球心为O,△BDC与△BDP外接圆的圆心分别为O1,02,则O,O2分别在线段QC,PQ的三等分点处(靠近点Q),连接OO002,易知O01⊥平面BCD,OO2⊥平面PBD,又平面PBD⊥平面BCD,四边形O01QO2为矩形.易知P-BCD外接球的球心为O,△BDC与△BDP外接圆的圆心分别为O1,O2,则O1,O2分别在线段QC,PQ的三等分点处(靠近点Q),连接O01,002,易知O0⊥平面BCD,OO2⊥平面PBD,又平面PBD⊥平面BCD,四边形OO1QO2为矩形.易知004=002=0Q=2QC=23,∴球O的半径R3,故三棱锥P-BCD外接球的表面积为4x(x13)2=解题关键》解决本题的关键:(1)能够知道三棱锥P-BCD的体积何时最大;(2)利用球半径、截面圆半径、球心到截面的距离之间的关系求出球半径