2022届智慧上进 名校学术联盟考前冲刺·精品预测卷(一)1理科数学答案

2022届智慧上进 名校学术联盟考前冲刺·精品预测卷(一)1理科数学答案，目前我们已经整理了2022届智慧上进 名校学术联盟考前冲刺·精品预测卷(一)1理科数学答案的各科答案和试卷，更多智慧上进请关注本网站。

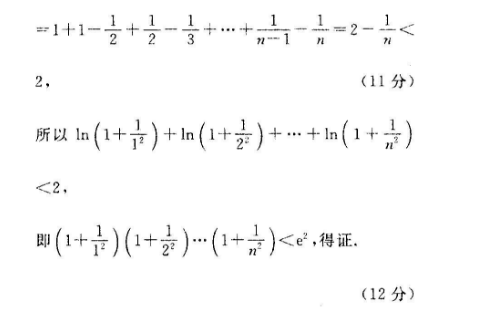
21.解:(1)由f(x)=n(x+1),可得f(x)=1代入切点横坐标x=0,得切线斜率k=1,所以切线g(x)=x(2分)it h( x)=f(x)-g(r)=In(c+1)x则h(x)=所以x∈(-1,0)时,h(x)>0,h(x)单调递增,x∈(0,+∞)时,h(x)<0,h(x)单调递减,所以h(x)mx=h(0)=0故h(x)≤h(x)mx=0,即f(x)≤g(x)(5分)(2)由(1)可知ln(x+1)≤x对任意的x>-1恒成(6分取x=广,有m(1+)<1取x=,有ln(1+取x=-,有ln(1+) <则ln(1+)+ln(1+a)+…+ln(1+)<1(8分)而1++…+<1+=1+1-1+1-1+…+-1-1=2-1<(11分)所以ln(1+)+ln(1+)+…+ln(1+即(+)(+2)(1+)<,得证(12分)< p>

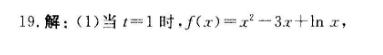
19.解:(1)当t=1时,f(x)=x2-3x+lnx,所以/(x)=2x-3+2x2-3x+1(2x-1)(x-1)令f(x)=0,x=或1,(2分)当0 0;当 2时,f(x)>0,所以当x=2时,(x)取得极大值,为-4-1n2当x=1时,f(x)取得极小值,为一2.(5分)(2)存在x0∈[1,e],使得f(xn)≥g(x。)成立,即存在x。∈[1,e],使得x-(2t+1)xa+lnx≥(1t)x0成立,则存在x∈[1,c],使得t≤x+-2,(8分)令h(x)=x×1nx-2,x∈1,e」,所以h'(x)=1+(10分)所以h(x)=1+1mx>0,(10分)所以函数h(x)在区间[1,e]上单调递增,即h(x)mhCe=c+所以≤e+1-2,即t的最大值为e+1-2(12分)