2022智慧上进高三数学押题答案

2022智慧上进高三数学押题答案,目前我们已经整理了2022智慧上进高三数学押题答案的各科答案和试卷,更多智慧上进请关注本网站。



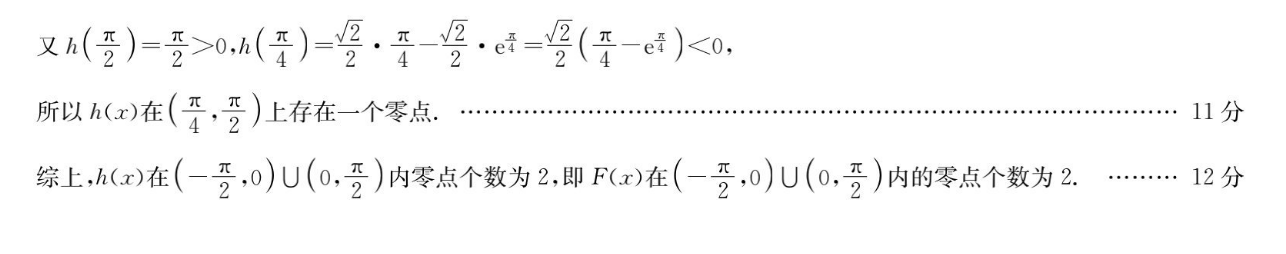
22解:(1)函数f(x)=的定义域为{x|x≠0},f(xece令f(x)=0,得x=1分当x∈(-∞,0)时,f(x)<0;当x∈(0,1)时,f(x)<0;当x∈(1,+∞)时,f(x)>0,所以f(x)在区间(一∞,0),(0,1)上单调递减,在区间(1,+∞)上单调递增5分(2)令F(x)=f(x)-g(x)=etan x=0, xsin x-e cos x=0设h(x)= asin- e cos a,所以h'(x)=(e+1)sinx+(x-e)cosx.①当x∈(一2,0)时,可知c>0>x,则c>,所以x-e<0,又sinx<0,08x>0,所以h(x)<0,从而A(x)= .rsin.-cosx在(一要,0)上单调递减,又A(0)=-1,(-2)=2>0由零点存在定理及h(x)的单调性,得h(x)在20上有一个零点……………7分②当r∈(0.]时,e≥inx>0,由(1)知函数f(x)=在(,1)上单调递减,在(,+∞)上单调递增,所以x∈(,时函数(x)=>f(1)=>1,则c>x≥>0所以 e cos r> asin,则h(x)= asin- e cos r<0恒成立所以h(x)在(0,上无零点分③当x∈(x,)时,sinx>os8x>o,n(x)=c(sinx-(sx)+(xosx+sinx)>0,则A(x)在(,受)上单调递增又(2)=2>0,()一·至一·=(-1)所以(x)在(,)上存在一个零点…………………………11分综上(x)在(一2,)(0,2)内零点个数为2即F()在(一2,0)U(0)内的零点个数为212

8.D因为等比数列{an}的各项均为正数,由a6+a7>a6a7+1>2,得(a6-1)(a-1)<0,因为a1>1,若a6<1,则一定有a7<1,不符合题意,故a6>1,a7<1,所以0






