2022智慧上进文科数学八答案

2022智慧上进文科数学八答案,目前我们已经整理了2022智慧上进文科数学八答案的各科答案和试卷,更多智慧上进请关注本网站。


9.【答案】A命题意图】本题考查基本不等式的应用【解析】令a+1=m,b+21,n>2,且a=m所以(n-2),(m-1)2(3-m)2(4-n)q+1b+29-6m+m16-8n+n29166+m+8+n91614+n6m)(m+n)-9=÷(9+16)-919n164当且仅当即3n=4m时等号成所以的最小值是一,故选Aa+1b+2
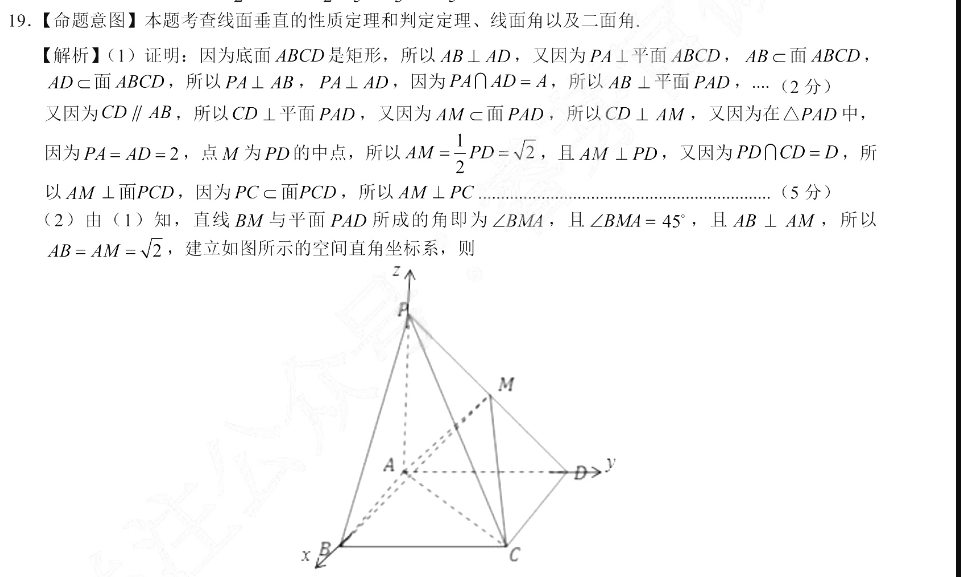
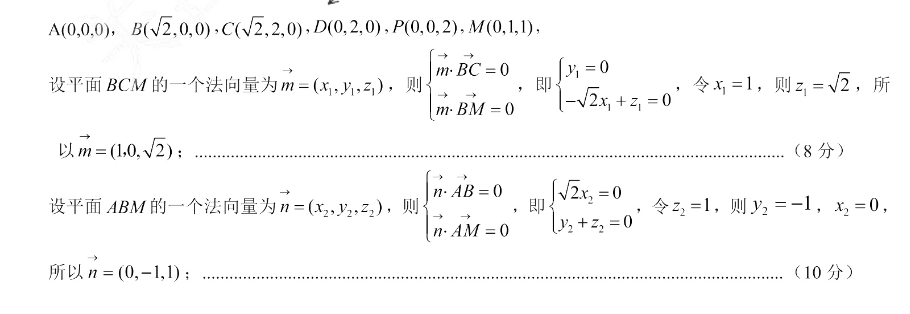
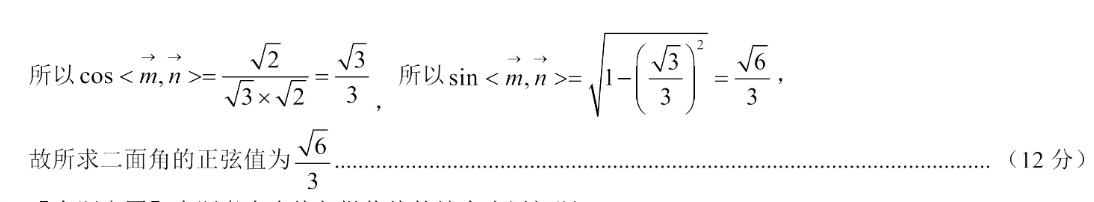
19.【命题意图】本题考查线面垂直的性质定理和判定定理、线面角以及二面角【解析】(1)证明:因为底面ABCD是矩形,所以AB⊥AD,又因为PA⊥平面ABCD,ABC面ABCDADc面ABCD,所以PA⊥AB,PA⊥AD,因为PA∩AD=A,所以AB⊥平面PA2分)又因为CD∥AB,所以CD⊥平面PAD,又因为AMc面PAD,所以CD⊥AM,又因为在△PAD中,因为PA=AD=2,点M为PD的中点,所以AM=PD=√2,且AM⊥PD,又因为PD∩CD=D,所以AM⊥面PCD,因为PCc面PCD,所以AM⊥PC(5分)(2)由(1)知,直线BM与平面PAD所成的角即为∠BMA,且∠BMA=45°,且AB⊥AM,所以AB=AM=√2,建立如图所示的空间直角坐标系,则MA.A(0,0.0),B(√2,00)C(2,2,0),D(O,2.0),P(0,0,2),MOBC=0设平面BCM的一个法向量为m=(x,y1,z1),则m·BM=0以m=(1,0,√2)(8分)·AB设平面ABM的一个法向量为n=(AM=0所以n=(0,-1,1)(10分所以cos






