2022智慧上进高考文数答案

2022智慧上进高考文数答案，目前我们已经整理了2022智慧上进高考文数答案的各科答案和试卷，更多智慧上进请关注本网站。

16.①③【命题意图】本题考查几何体的外接球和内切球、几何体的体积,考查转化与化归思想,体现了逻輯推理、数学运算、直观想象等核心素养【解析】设该几何体的外接球的半径为R,则4πR2=36丌,解得R=3.根据①作出该几何体的轴截面图,如图(1).设圆柱与圆锥的高都为h,底面半径为r,则3h=2R=6,h=2,;r2=R=9-1=8,∴该几何体的体积v=7h+2×1x2h=5m7h=5m×8×2=80m,①正确根据②作出该几何体的轴截面图,如图(2),当该几何体的轴截面(过旋转体轴的截面)为正六边形时,其内切球的半径r=3R,,=外接球RR=8…②错误记该几何体外接球球心为O,则点O到轴截面六个顶点的距离都相等,均为R,由O与六个顶点连线分割的六个三角形都是等腰三角形,若此时该几何体又有内切球,则其内切球球心必须与外接球球心重合,点O到六条边的距离要相等,且为内切球的半径,因此这六个等腰三角形全等又六个等腰三角形的顶角和为2丌,…六个等腰三角形都为等边三角形,轴截面为正六边形,∴③正确图(1)图(2)≌名师评题本相当于一道多项选择题,信息量大,知识点多,综合性强.本题背景新颖,所给的几何体是由两个圆锥和一个圆柱组成的组合体,进而考查这个组合体的外接球和内切球,一道几何题考查了多个几何体,体现了试题注重在知识交汇处命题的指导思想本题对空间想象能力、数学抽象能力、推理论证能力、数学运算能力都有较高的要求,能很好地考查学生的创新能力和灵活应变能力,以及综合运用知识解决问题的能力

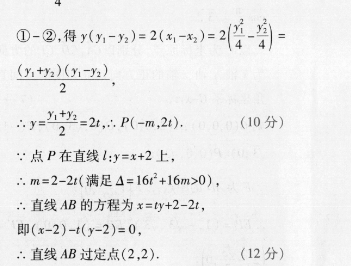
21.【命题意图】本題考查拋物线的标准方程、直线与拋物线的位置关系、直线过定点问题,考查数形结合思想、转化与化归思想,体现了逻辑推理、数学运算、直观想象等核心素养(1)【解]:抛物线C:y2=2mx(p>0)上一点(x02)到焦点的距离为2,xn+2=2解得p=2(3分2px=4,抛物线C的标准方程为y2=4x,(4分(2)【证明】设直线AB的方程为x=y+m,A(x1y1),B(x2,y2)由y=4x,消去x并整理,得y2-4y-4m=0x=ty+n=16r+16m>0,y1+y2=41,y1y2=-4m(6分)∵y2=4x,…当y>0时,y=2x,此时y==2;当y<0时,y=-2,此时y=-1=2过抛物线上一点(x0,%0)(x0≠0)的切线方程可表示为y-y0=-(x-x),即ya=2(x+x0)(当切线过原点时也符合),切线PA的方程为y1=2(x+x1),切线PB的方程为y2=2(x+x2)(9分)联立得方程组y2=2(x+x2).②①.得二x+3,即x(y1-y2)=xy-2y1=24(y1-y2),①-②,得y(y1-y2)=2(x1-x2)=2(y1+y2)(y1-y2)2y1+y22=2t,P(-m,2)(10分)∵点P在直线l:y=x+2上,∴m=2-2(满足A=16t2+16m>0),∴直线AB的方程为x=y+2-2t,即(x-2)-t(y-2)=0,∴直线AB过定点(2,2)(12分)