智慧上进2021答案理综5

智慧上进2021答案理综5，目前我们已经整理了智慧上进2021答案理综5的各科答案和试卷，更多智慧上进请关注本网站。

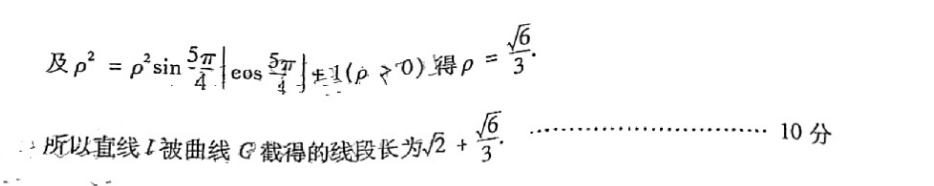
22.解：(1)C的极坐标方程为p2=p2sin01cos01+1.设A(pu,c),则p=pisinI cos+1=sinco+1,a∈1y,Z】又B的极坐标为P,a+）,将B的极坐标代入C的极坐标方程得p=pisin(a+eo(a++1=sinco+l,ae(0,》即B的极坐标满足C的极坐标方程，故点B在曲线C上.…5分(2)将直线1的参数方程：=‘化为极坐标方程为0=平(p∈).y=.代人C的极坐标方程得。2=sin牙os平+1(p>0)得p=万及m=pan7智生e0)器p-停所以直线1被曲线C截得的饿段长为2+…10分

19.(1)证明：由题可知：∠BAD=∠BAC+∠CAD=90°，即AD⊥AB又PD2=PA2+AD2→AD⊥AP且AB、AP是平面PAB内两相交直线故AD⊥平面PAB.……6分(2)解：当N为PD中点时，取AD的中点Q,连接QN、CQ,则QN平行于PA,CQ垂直于AD,可得CQ平行于AB,故平面CQN平行于平面PAB,所以CN∥平面PAB,即当N为PD中点时，CN∥平面PAB.所以，c=子e=子，@m由(1)知PA就是三棱锥P-ACD的高所以m=号x5a×PA=青×7x尽x号x1=9故多面体P-MNC的体积为号n分