智慧上进2021数学理科七答案

智慧上进2021数学理科七答案，目前我们已经整理了智慧上进2021数学理科七答案的各科答案和试卷，更多智慧上进请关注本网站。

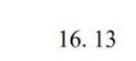
16.13

21.解:(1)当a=1时,f(x)=·(x+sinx-2-2)①r(x)=(x+imnx+0sx-2-1),(0)=-2-2,/(0)=-2则曲线y=f(2)在点(0,f(0)处的切线方程整理为y=-2x-2-23分②令g(x)=x+sinx+cosx1,有g(x)=1+cosx-sinx=1-√2sin(x当一x≤x≤2时,g(x)≥0,g(x)单增,g(x)≤g(2)=0,得f(x)≤0同理当≤x≤x时,g(x)≤0,(x)≤g()=0,可得f(x)≤0,故函数f(x)在区间[一π,r]上递减分(x)m=f(x)=e(2-2)(3r+4)e故函数f()在区间[一x上的值域为[(二),一3x+47分2)由0 f(x)-(a-2-2)e即函数G(x)=f(x)-(a-2-2)e=c(ax+sinx-a)在区间(0,x)上为增函数G(x)=e(ax+sinx+cosx),故当x∈[0,r]时,G(x)≥0,即ax+sinx+cosx≥0恒成立②当0 0,有h(x)<0当1 0,有h(x) <即函数h(x)单调递减,故h(x)min=h(x)=故有一a≤得< p>