2022智慧上进理科数学答案

2022智慧上进理科数学答案，目前我们已经整理了2022智慧上进理科数学答案的各科答案和试卷，更多智慧上进请关注本网站。

22【解析】(1)由P=√3sn(个一得psin(-x)=1,即psin0-pcos0=1,整理得直线l的直角坐标方程为3x-y+2=0分由{2得椭圆E的普通方程为2+y=1ly=sing(2)由(1)知直线l的斜率为3,故其倾斜角为3故可设直线l的参数方程为(t为参数6分/3将直线的参数方程代入+y2=1中整理得72+163t+24=0,163易得△=96>0,设方程的两根分别为t1,t2,则t1+12=-7,12=78分+t√3所以QMAB|=1t1-t21|=√(1+42)2-41t22IQMI所以LABI√210分

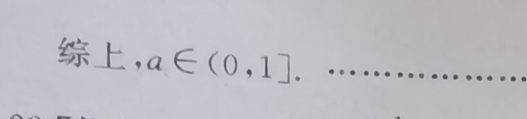
21.【解析】(1)f(x)在(1,+∞)上单调递减2分证明:因为f(x)1分所以x≠0且f(x)(x)=(12分当x∈(1,+∞)时,m(x)<0,函数m(x)单调递减所以m(x) 0,所以e2+a>04分又因为(e2+a)f(x)≥2a,所以f(x)所以所以e+a1≥0设h(x)=2a(e5分eT a,则h(x)≥0易知当x<0时0;当0时设2a(则6分且g(x)2a2e+e(e2+a)22①当a2-a4≥0即0 0;当x>0时,g(x)>0,所以h(x)>0故(e2+a)f(x)≥2a8分②当a>1时,因为g(x)=(c)2-2a2e+,设p(x)=(e2)2-2a2e+a2,当x∈(0,ma2)时,t=e∈(1,a2),则t2-2a2t+a2<0,所以g(x)<0,故g(x)单调递减,结合g(0)=0知g(x)<0,所以h(x)<0,不合题意,舍去10分信息押题卷(三)全国卷1理科数学答案第5页(分综上,a∈(0,1