2022智慧上进高二数学2-2答案

2022智慧上进高二数学2-2答案，目前我们已经整理了2022智慧上进高二数学2-2答案的各科答案和试卷，更多智慧上进请关注本网站。

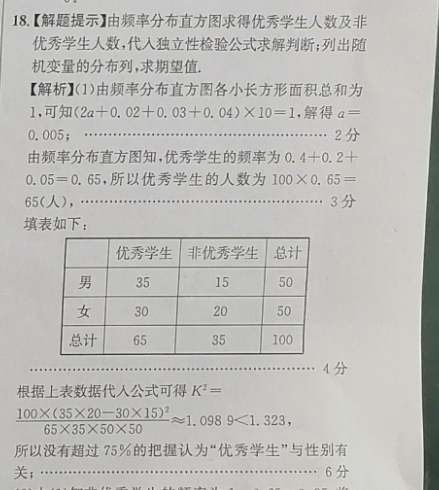
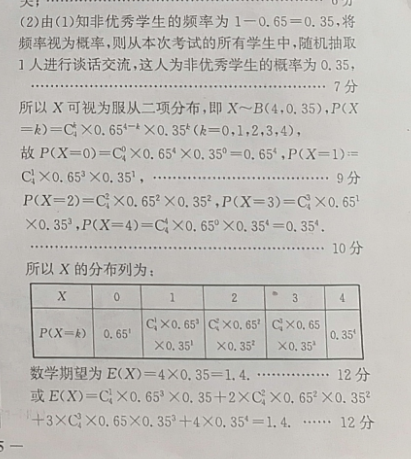
18.【解题提示】由频率分布直方图求得优秀学生人数及非优秀学生人数,代入独立性检验公式求解判断;列出随机变量的分布列,求期望值【解析】(1)由频率分布直方图各小长方形面积总和为1,可知(2a+0.02+0.03+0.04)×10=1,解得a=0.005;………2分由频率分布直方图知,优秀学生的频率为0.4+0.2+0.05=0.65,所以优秀学生的人数为100×0.6565(人),3分填表如下:优秀学生非优秀学生总男351550女总计65351004分根据上表数据代入公式可得K2=100×(35×20-30×15)2≈1.0989<1.32365×35×50X50所以没有超过75%的把握认为“优秀学生”与性别有关6分(2)由(1)知非优秀学生的频率为1-0.65=0.35,将频率视为概率,则从本次考试的所有学生中,随机抽取人进行谈话交流,这人为非优秀学生的概率为0.35…………7分所以X可视为服从二项分布,即X~B(4,0.35),P(X=k)=C×0.654-×0.35(k=0,1,2,3,4),故P(X=0)=C×0.654×0.350=0.654,P(X=1)=C×0.653×0.351,………………9分P(X=2)=C4×0.6532×0.352,P(X=3)=C×0.6510.353,P(X=4)=C4×0.65×0.35=0.35…………………10分所以X的分布列为P(X=k)0.65C×0.653c×0.65c×0.65×0.35×0.352×0.30.35数学期望为E(X)=4×0.35=1.412分或E(X)=C×0.653×0.35+2×C4×0.652×0.352+3×C×0.65×0.353+4×0.354=1.412分

19.【解题提示】由线面垂直的判定及性质证得PD⊥BC,结合BC⊥BD,可得BC⊥平面PDB,建立空间直角坐标系,利用空间向量求二面角【解析】(1)由BC⊥BD,AD∥BC,所以AD⊥BD,又平面PAD⊥平面ABCD,平面PAD∩平面ABCDAD.BD二平面ABCD故BD⊥平面PAD,得BD⊥PD,………2分由AD=PD=1,AP=2得,AD+PD=AP2,即PD⊥AD,又因为AD∩BD=D,所以PD⊥平面ABCD,分由BCC平面ABCD,得PD⊥BC又因为PD∩BD=D所以BC⊥平面PDB分(2)由(1)可知,PD,AD,BD两两垂直,AD=BD=PD=1,如图,以D为坐标原点,DA所在直线为x轴,DB所在直线为y轴,DP所在直线为z轴,建立空间直角坐标系Dxyz则P(0,0,1),A(1,0,0),B(0,1,0),C(-1,1,0),所以PA=(1,0,-1),PC=(-1,1,-1),PB=(0,1,7分设n=(x1,y,z)为平面APC的法向量则PA=O即21+y-2=0可取n=(1,2,1)9分设m=(x2,y2,=2)为平面PCB的法向量则PB即0可取m=(0,1,1),10分故cosm,n)=Tm因为二面角APCB为锐二面角,所以二面角APCB的大小为12分【易错提醒】正确选择坐标轴,建立空间直角坐标系Dxy,写出相关点坐标、向量,求出法向量及其夹角