智慧上进数学2021答案

智慧上进数学2021答案，目前我们已经整理了智慧上进数学2021答案的各科答案和试卷，更多智慧上进请关注本网站。

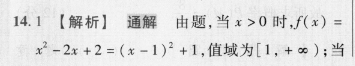
14.1【解析】通解由题，当x>0时，f(x)=x2-2x+2=(x-1)2+1,值域为[1，+)；当x≤0时f代x)=-x+a,值域为[a,+o).故a≥1,a的最小值为1，优解作出函数f(x)的大致图象如图所示，数形结合可知，要使f(x)的值域为[1，+∞)，则a≥1，所以a的最小值为1.

20.【解题思路】(1)由题f(x)的定义域为(0，+∞)，f'(x)=(x+1)(ax-1)对a分情况讨论函数f八x)的单调性(2)f()≥a2+(a-1)x-ae一a≥+1构造面然设g(x)血+1→g'(x）=ee1-1nx-1e种造西数设h(x)=-nx-1一h(x)在(0，+x)上单调递减1)=0，g()的单调性一g(x)≤g1)=。1e解：(1)由题意知函数f(x)的定义域为(0，+∞)，f'(x)=ax+(a-1)-1=x+1)(ax-1)(2分)若a≤0，则f'(x)<0,f(x)在(0，+∞)上单调递减；(3分)若a>0,则当xe(0,)时，f'(x)<0,当x∈(合+)时f"()>0,所以(x)在(0，)上单调递减，在(，+0)上单调递增。（分类讨论时，一定要选好分类讨论的标准，微到不重不漏)(5分)综上，当a≤0时f(x)在(0，+∞)上单调递减；当a>0时，f(x)在(0，)上单调递减，在(。，+∞)上单调递增.(6分)(2)fx)≥2ar2+(a-1)x-ae即ae'≥lnx+1,即a≥血x+1(分离参数)(7分)⊥-lnx-1设g()=血，则g()-e(8分)设h(x)=-lnx-1,易知h(x)在(0，+0)上单调递减，且h(1)=0,所以当x∈(0,1)时，h(x)>0,即g'(x)之0，g(x)单调递增；当x∈(1，+0)时，h(x)<0,即g(x)<0,g(x)单调递减.（提示：e>0)(10分）故g(x)≤g(1)=1,所以a≥1(11分)故a的取值范围为[二，+0)(12分)⑩临考妙招对于含参的不等式恒成立问题，一般要借助导数的知识以及函数的单调性等，采用数形结合思想求解，常用的方法有分类讨论法、分离参数法以及等价转化法等，