2022名校学术联盟高考模拟信息卷数学十一答案

2022名校学术联盟高考模拟信息卷数学十一答案，目前我们已经整理了2022名校学术联盟高考模拟信息卷数学十一答案的各科答案和试卷，更多智慧上进请关注本网站。

13.3因为直线y=2x-3过抛物线C的焦点，所以号=三，故力=3.

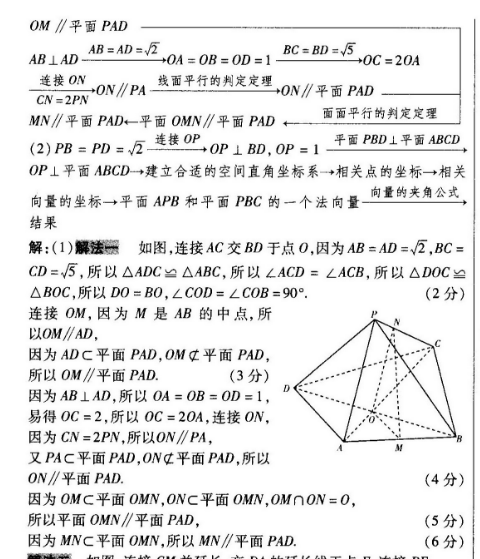
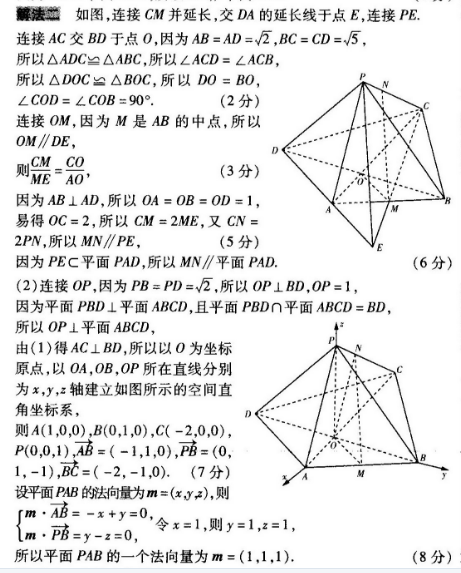
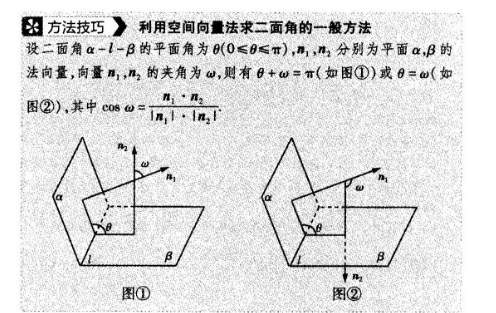
20.【关键能力】本题考查逻辑思维能力、空间想象能力和运算求解能力【学科素养】试题以四棱锥为载体,利用数学语言描述图形的特征,引导考生利用所学的几何知识探求线面位置关系,并利用向量法求解二面角的正弦值,考查理性思维、数学探索等学科素养.【解題思路】(1)AB=AD=√2,BC=CD=√5→△ADC≌△ABC连接AC交BD千点O∠ACD=∠ACB→△DOC≌△BOC→DO=B0OCOD=∠COB=9°、连接OM→OM∥MD、线面平行的判定些OM∥平面PADAB=AD=,2AB⊥ADBC=BD=5→OA=OB=OD=1+OC=20A连接ON线面平行的判定定理→ON∥平面PADMN∥平面PAD←平面OMN∥平面PAD面面平行的判定定理(2)PB=PD=2连接O→OP⊥BD,OP=1平面PBD⊥平面ABCDOP⊥平面ABCD→建立合适的空间直角坐标系→相关点的坐标→相关向量的坐标→平面APB和平面PBC的一个法向量向量的夹角公式结果解:(1)解法一如图,连接AC交BD于点O,因为AB=AD=√2,BC=CD=5,所以△ADC≌△ABC,所以∠ACD=∠ACB,所以△DOC≌△BOC,所以DO=BO,∠COD=∠COB=90°(2分)连接OM,因为M是AB的中点,所以OM∥AD,因为ADC平面PAD,OM￠平面PAD,所以OM∥平面PAD(3分因为AB⊥AD,所以OA=OB=OD=1,易得OC=2,所以OC=2OA,连接ON,因为CN=2PN,所以ON∥PA又PAC平面PAD,ON￠平面PAD,所以ON∥平面PAD(4分)因为OMC平面 OMN, ONC平面OMN,OM∩ON=0所以平面OMN∥平面PAD(5分)因为MNC平面OMN,所以MN∥平面PAD(6分)解法如图,连接CM并延长,交DA的延长线于点E,连接PE连接AC交BD于点O,因为AB=AD=2,BC=CD=5所以△ADC≌△ABC,所以∠ACD=∠ACB,所以△DOC≌△BOC,所以DO=BO,∠COD=∠COB=90°(2分)连接OM,因为M是AB的中点,所以CM CO(3分)因为AB⊥AD,所以OA=OB=OD=1,易得OC=2,所以CM=2ME,又CN2PN,所以MN∥PE,(5分)因为PEC平面PAD,所以MN∥平面PAD.(6分)(2)连接OP,因为PB=PD=2,所以OP⊥BD,OP=1因为平面PBD⊥平面ABCD,且平面PBD∩平面ABCD=BD,所以OP⊥平面ABCD由(1)得AC⊥BD,所以以O为坐标原点,以OA,OB,OP所在直线分别为x,y,z轴建立如图所示的空间直角坐标系,则A(1,0,0),B(0,1,0),C(-2,0,0)P(0,0,1),=(-1,1,0),座=(0,1,-1),b=(-2,-1,0).(7分)设平面PAB的法向量为m=(xx),则=-x+y=0令x=1,则y=1,z=1=y-z=0,所以平面PAB的一个法向量为m=(1,1,1)(8分)设平面PBC的法向量为n=(x1,y1,z1),则B=(x1,y,x1)·(-2,-1,0)=-2x1-y=0,n·PB=(x1,y1,x1)·(0,1,-1)=y1-z1=0,令x1=1,则y1=-2,x1=-2,所以平面PBC的一个法向量为n=(1,-2,-2)(10分)所以cos(m,n)=mn(11分)设二面角A-PB-C的平面角为,则如=、1-(-4)2=方法技巧》利用空间向量法求二面角的一般方法设二面角a-l-B的平面角为6(0≤6≤T),m1,n2分别为平面a,B的法向量向量m,n2的夹角为a,则有日+am(如图①)或6=(如困②),其中coso=图①图②