2022智慧上进2020答案数学文

2022智慧上进2020答案数学文，目前我们已经整理了2022智慧上进2020答案数学文的各科答案和试卷，更多智慧上进请关注本网站。

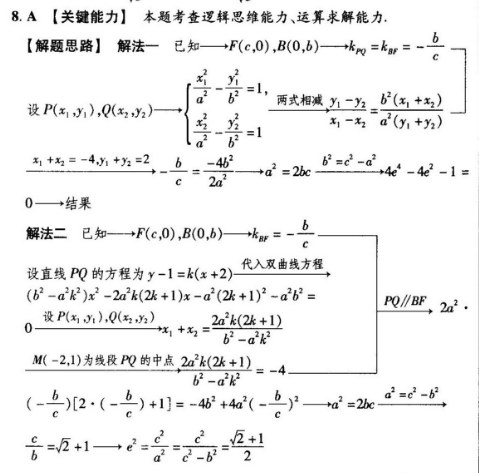
A【关键能力】本题考查逻辑思维能力、运算求解能力【解题思路】解法一已知一→F(e,0),B(0,b)-+=kn=-b设P(x1y1),Q(x2,y2)两式相减y1-y2b2(x1+x2)x1-x2a2(y+y2)x1+x2=-41+y2=2b-452b2=c2-a20—→结果解法二已知一→F(0),B(O,b)+kn=-b设直线PQ的方程为y-1=k(x+2)代入双曲线方程(b2-a2k2)x2-2a2k(2k+1)x-a2(2k+1)2-a2b2=设P(x11),Q(x,y2)02a2k(2k+1)B-aK2M(-2,1)为线段PQ的中点2a2k(2k+1)B2-ak(-b)(2·(-b)+1]=-462+42(-b)2【解析】解法由题意知F(c,0),B(0,b),则设P(y1),Q(x2,y2),则221x两式相减,得22因为线段P的中点为M-2,1),所以x+=-4,+y2=2,又k=2=-2x1-x2所以-b=二4,整理得a2=2k,所以a=4b2=4(2-a2),即4-42-1=0,得2=2+1,故选A解法型由题意知Fe.O,B(0.b,则和=-b.设直线P的方程为y-1=k(x+2),即y=kx+2k+1,代入双曲线方程得(b2-a2k2)x2-2n2k(2k+1)xa2(2k+1)2-a2b2=0.设P(x1,y1),Q(x2,y2),则x1+x2=-4,所以2n2k(2k+1)b2-a32=-4又k=km=-b,所以2·(-b)12.(-b)+1=4+4(-2),整理得d2=2b,所以2-62-2=0,即(合(x)20,得=2+1,则c2(2+1)22+1(2+1)2-1=2,故选A羽结论拓展》求双曲线离心率常见的方法:①根据巳知条件列方程组,解出a,c的值,直接利用离心率公式求解;②根据已知条件得到一个关于a,(或a,b)的齐次方程,然后转化为关于离心率e的方程来求解

16.25-5【解析】解法一：由题可知∠BBG=10120°，且BB,=B1G=2a,所以∠B1GB=30°，又B1C=a,B1G=2a,∠C,B1G=90°，所以C1G=5a,从而im∠8，CG-=晨。=停cos∠BGC-5a2兰=25，所以cos∠C,GB=cos(∠CGB,+30)5a5=cos∠C,GB,cos30°-sin∠C,GB,sin30°=2￥55号-9x含25解法二：连接BC1,∠BB1C1=150°，BB1=2a,B,C1=a,所以由余弦定理得BC=BB十B,C一2BB1·BGos150=4+a+2×2aXax号=50+解法二：连接BC,∠BB1C=150°，BB1=2a,BC1=a,所以由余弦定理得BC=BB十BC-2BB,·B,C cos150'=4a2+a2+2X2a×a×号=5a+2√3a2,又BB,=B1G=2a,∠BB1G=120°，所以BG=2√3a,C1G=√5a,所以在△BCG中由余弦定理得cos∠C,GB=BC+CC-BG2BG·C1G12a2+5a2-5a2-23a2_25-52X2√3a·√5a10