2022名校学术联盟2020数学八答案

2022名校学术联盟2020数学八答案,目前我们已经整理了2022名校学术联盟2020数学八答案的各科答案和试卷,更多智慧上进请关注本网站。



22.(1)证明:当a=一b=1时,f(x)=xe.令h(x)=e一(x十1)(x>0),则h'(x)=e-1>0,所以h(x)在(0,十∞)上单调递增,且h(0)=0,所以h(x)=e一(x十1)>0,即e>x十1.…1分令p(x)=x-lnx(x>0),则p(r)=1-】=二1,所以g(x)在(0,1)上单调递减,在(1,十o)上单调递增,且o(1)=1,所以(x)=x一lnx≥1>0,所以江>n,…2分所以当x∈(0,十o∞)时,有xe>x(x十1)>(x+1)lnx,所以当x∈(0,十0∞)时,f(x)>g(x).…4分(2)解:因为3b∈[一1,0],使f(x)≥g(x)恒成立,令(b)=axe+(a十b)x,只需(b)mx≥g(x),即a.xer十ax≥(1十x)lnx在x∈(0,十o∞)上恒成立,…6分整理得a.x(e十1)≥(x十1)lnx=lnx(enr十1).(*)…7分设F(x)=x(e十1),则F(x)=e(x十1)十1.…8分又F"(x)=(x十2)e,可得x>一2时,F"(x)>0,F(x)单调递增:x
<一2时,f"(x)<0,f(x)单调递减,因此当x=-2时,f'(有最小值f'(-2)=1-专>
0,所以F(x)在R上单调递增。……10分所以(*)式即F(ax)≥F(lnx),所以ax≥lnx,即a≥n11分设G(x)=1n,x>0,则G(x)=1-h工,令G(x)=0,解得r=e.当0

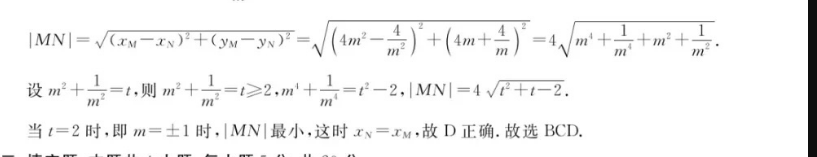
12.【答案】BCD【解析】设A(x1,y1),B(x2,y2),E(x,ya),D(x4,y),M(xM,yM),N(xN,yN),直线l1的方程为x=y十2.则直线,的方程为=一品十2.将直线l1的方程x=my十2代人y2=8.x,化简整理得y2一8my一16=0,则y1十y2=8m,y1y2=一16,故x,十2=m(y十为)十4=8m2+4.所以x4==4m2十2,yw=业=4m.2因为点A到直线l的距离d,=x1+2,点B到直线l的距离d:=x2十2,点M到直线I的距离dM=xM十2,又xM=4m2十2,所以dw=4m2十4,故A错误:因为AB=AF|十BF=x1十x2+4=8m2+8=2dM,所以以|AB为直径的圆的圆心M到1的距离为A,B,即以AB为直径的圆与1相切,故B正确:2同理函十=-(%十)+4=8+4,所以xw=清+2w=-点ED=EF十1DF=+x+4=8+8,则|AB1+|ED=8m2+8一+16≥32,当且仅当m=士1时等号成立,故C正确:MN=aw-+(w-=√m-)+(m+)=4Vm++m+.设m+=4,则m+0=≥2,m+d=f-2,MN=4V+1-.当t=2时,即m=士1时,|MN|最小,这时xx=xM,故D正确.故选BCD.






