2022届智慧上进·名校学术联盟 高考模拟信息卷 押题卷(九)9理科数学试题答案

2022届智慧上进·名校学术联盟 高考模拟信息卷 押题卷(九)9理科数学试题答案,目前我们已经整理了2022届智慧上进·名校学术联盟 高考模拟信息卷 押题卷(九)9理科数学试题答案的各科答案和试卷,更多智慧上进请关注本网站。



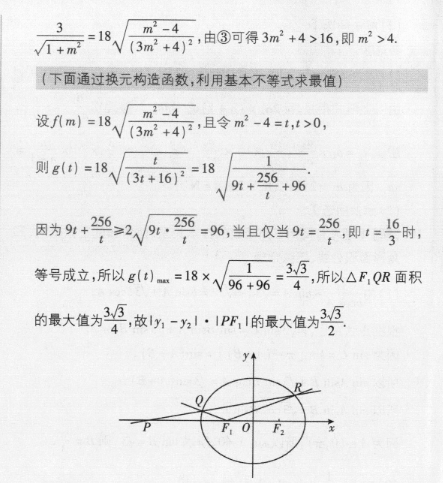
21.【思路导引】(1)由斜率公式求出k1,,一·的值求出c→得a,b的关系式解方程组求→得解:将点M的坐标代入椭圆方程出a,b的值得a,b的关系式(2)将问题转化为求Srm的最大值→设直线QR的方程式为x=m四y+n(m≠0)→联立椭圆方程-根与系数的关系斜率互为相反数+求出n的点到直线的值距离公式写出Sarw的表达式构造函数,由基本不等式得解【解】本题考查椭圆方程、直线与椭圆的位置关系(1)由题意知F(-c,0),F2(c,0),2(5+c)2(5-c)所以由66=号,得5.-332(5+c)2(5-c)8'解得c=1,所以a2-62=1.①将点M5,-受))的坐标代入椭因方程,得子+*46=1,②由①②联立,解得a=2,b=√5,所以椭圆C的方程为香+兮=1.(2)由题意可画出图像如图所示,此时y2>y1>0,则(下面将线段关系转化为三角形面积问题)ly1-%I·IPFI=IIPF,I·y-IPFI·yI=2 ISAPER-S△Pr01=2SaP.0R(设直线方程时为避免讨论,考虑将直线方程设为x=my+n的形式)设直线QR的方程为x=my+n(m≠0),代入椭圆方程,得(3m2+4)y2+6my+3n2-12=0,所以4=36m2n2-4(3m2+4)(3n2-12)>0,可得n2<3m2+4.③6mn由根与系数的关系可得+为:34-孤由题意知(-1,0,所以行在=0,室理得++x2y1+y1=0.将,1=my,+n,名2=my2+n代入上式,得2my3+(n+1)(y1+万0,所,-,解得=4,所以QR的方程为x=my-4,即x-my+4=0.(下面利用点到直线的距离公式求出Srm的表达式)因为点F(-1,0)到直线QR的距离d=1-1-0+41√1+m2=18√(3m2+4,由8可得3m2+4>16,即m2>4.m°-4(下面通过换元构造函数,利用基本不等式求最值)设f八m)=18m2-4(3m2+4,且令m2-4=1,t>0,则g=18√(3+16=1819+26+96t因为9+的>2√9·-96,当且仅当9=0,即13时,1133等号成立,所以g刊=18×√96+96=4,所以△R,QR面积的最大值为3,故1,-1·PR,1的最大值为3F


10.BD【解析】本题考查对数函数的图像与性质、函数的奇偶性对于A选项,由题意得1g,3=-1,所以a=了,所以A不正确:对于B选项,由题意知0<1g(2-2x)<1,等价于1<2-2x<10,解得-4






